Cats on Keyboards – 221B-01 Unit 221B is a remote business, and working from home is commonplace....
How to Share a Secret… Secretly
Great in Theory
In November of 1979, Adi Shamir published the paper “How to Share a Secret” where he came up with a mathematical method for dividing data (D) into n pieces in such a way that that D is easily reconstructed from any k pieces, and yet even complete knowledge of k-1 pieces reveals absolutely no information about D.
The advantage to this was robust key management schemes for cryptographic systems that can function securely and reliably even when misfortunes destroy half the pieces and security breaches expose all but one of the remaining pieces. This paper can be found here.
In a time where it seems that Shamir (or derivatives from such work) Secret Sharing Protocols don’t seem practical compared to multi-signature (as seen being deployed by coin-based protocols to authorize multi-party transactions), We were pondering over the problem of practical systems that could use this without the overhead of public-key cryptography.
Let’s take a step back
Here’s a quick primer that anyone can do in Linux to demonstrate Shamir’s Secret Sharing Scheme (SSSS for short).
sudo apt install ssss
Once that’s installed take a look here at the man page for “ssss”. We can see there is are two main binaries: “ssss-combine” and “ssss-split“. So the general idea is you would like to split a secret into multiple keys, with the idea that the secret can only be revealed when the minimum threshold of keys you assigned and handed out are put together to reveal the secret. Practical uses aren’t necessarily that great for data more than 128 bytes, since each key that’s split is the same size of the secret itself. So the ideal situation is AES-256 bit keys that you may hold the keys to the kingdom, or a bitcoin wallet.
Let’s show an example:
We have a key that we want to protect and split with 5 people, and when 3 of them come together they can unlock the key:
4f346b7253beaf423f8b7e163feb6715b3ec7f711059dcc3a611543a51dab31d
We can simply go to our Linux terminal and do this:
ssss-split -t 3 -n 5
Generating shares using a (3,5) scheme with dynamic security level.
Enter the secret, at most 128 ASCII characters: Using a 512 bit security level.
1-4d7800bdd593316b1b32fab55b78ebe6a99c54f866452379219dd1e1437e84652e4ea798e96a4889b3697b3b326b035b8a65643e75859d9cbc873225a1f97a84
2-f6a7b8b8e695354eadbec925e4435bc207e0a15d3227963e52ae08deaecdd9eb0561f2f4fc3991985b5072450a9a2fad53c760e48f6de7faa9fd5bc9b4bdf815
3-50e7cb6b93a812cdc1442084a6da672b3c606080d5f45bb001f270b8da105ce744523faa945236e6eb89ad8e0b7d221b49846e7bd33a76de1c7f6521652eb8aa
4-947b55009ddde325cd2982ba00e71aeb321222d916af90332943ad61c629fa061aa85098cccdd161573cad16aac0a4dfca7823c61ceefe12670509916600b6cc
5-323b26d3e8e0c4a6a1d36b1b427e26020992e304f17c5dbd7a1fd507b2f47f0a5b9b9dc6a4a6761fe7e572ddab27a969d03b2d5940b96f36d2873779b793f661
We would in theory, hand out a key to each individual for them to not lose. In the necessary situation that we needed to reveal the secret key, we would simply put at least 3 of the split keys together, like so:
ssss-combine -t 3
Enter 3 shares separated by newlines:
Share [1/3]: 1-4d7800bdd593316b1b32fab55b78ebe6a99c54f866452379219dd1e1437e84652e4ea798e96a4889b3697b3b326b035b8a65643e75859d9cbc873225a1f97a84
Share [2/3]: 2-f6a7b8b8e695354eadbec925e4435bc207e0a15d3227963e52ae08deaecdd9eb0561f2f4fc3991985b5072450a9a2fad53c760e48f6de7faa9fd5bc9b4bdf815
Share [3/3]: 3-50e7cb6b93a812cdc1442084a6da672b3c606080d5f45bb001f270b8da105ce744523faa945236e6eb89ad8e0b7d221b49846e7bd33a76de1c7f6521652eb8aa
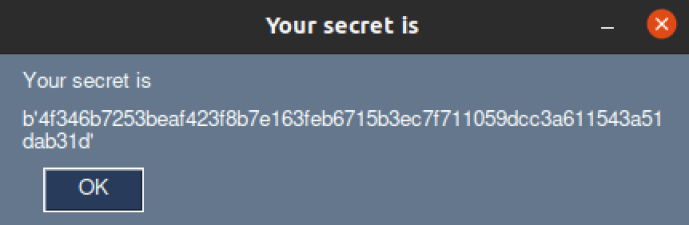
Resulting secret: 4f346b7253beaf423f8b7e163feb6715b3ec7f711059dcc3a611543a51dab31d
The Practical Upshot
Now in a world where we have public keys to which we can encrypt to each user, this scheme does not seem all that useful. Also, the cumbersomeness of the keys and the likelihood that someone would store these securely and such gets complicated very quickly. It would be not very practical to ask 3 people that were not tech savvy to hold onto these keys, and if they don’t know public key cryptography, they won’t store them securely. So is this scheme practical and can it be?
So we started looking at a way to not only share these secrets in a practical way, that could last a lifetime of secure archiving, but additionally, is there a way we could share these secrets without the other parties knowing they are holding onto a secret?
Disappearing Cryptography
The concept of Steganography (stego for short) is that of hiding secret messages in plain sight. This concept has been around for a long time, and the technology isn’t exactly new. Then again, neither are good cryptography algorithms. The most common technique is hiding data inside of images using a technique called Least-Significant Bit (LSB). This technique is simply security-by-obscurity, being the fact that you would have to have a reason to suspect that Alice, Bob or whoever would be deploying stego in the first place. Then one would also have to locate the image itself, and there are a bunch of other rabbit holes here. That said, security-by-obscurity has it’s place in information security…. what’s your password?
By combining the two concepts together, the secret sharing, and the hiding of messages, we are able to prove that one could hand out a secret, without the parties knowing it was a secret.
Example Scenario
Let’s make 2 files that we hand to party-1 and party-2 with a 2-key threshold:


The hidden data inside each of the files have been encrypted with AES-256-CBC with a password we know. For this example we kept it simple: a sha256 hash of our email address. Since our parties are none the wiser, this password is mainly for protecting the data inside the secret, in the case they learn there is one (unlikely).
Email Signature Policy
Inside these files is a secret message that we can hand to our parties, and tell the parties:
please use these files in your email signatures for our logo.
— Sincerely, Unit 221B 😉
The parties simply put these files in their email as expected with corporate policy, unknowingly carrying a secret the entire time.
Since these logos will be seen in emails by our parties, we can always access them as they are archived in emails. Additionally, anyone they email will also have them archived. By doing this, we create an eloquent password management solution for an unmemorable secret that can be accessed as needed by the parties simply emailing a reply along with a dependable and persistent archival rate. No public keys, no worrying about whether they will handle the secret safely and no worries about likely expiration. The parties involved are simply unaware couriers ensuring our secret.
When we run the code with the two files from the email and enter our password:
The full code can be found here. Have fun!
